Imagine que você queira descrever em que posição um objeto se encontra em uma linha orientada. Esta linha pode ser uma auto-estrada assim como o objeto pode ser o automóvel.
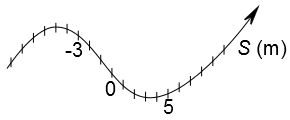
A figura acima representa um referencial orientado que pode ter qualquer formato: pode ser uma auto-estrada e pode até mesmo ser uma curva fechada como o contorno de um lago. É também orientado, o que significa dizer que em certa direção, ao longo da curva, ela terá sentido positivo e em outra, terá sentido negativo. Na verdade, é como se você tivesse uma reta real que se "entorta" acompanhando a curvatura que sesejar.
Imagine que em determinado instante, você esteja na posição -3 m, ou seja, segundo nossa figura, você está três metros à esquerda do "marco zero". Este "marco zero" é chamado de origem dos espaçoes! Vamos chamar de $S_0$ a posição inicial e $t_0$ o instante inicial, isto é, quando olha para o relógio e tem consciência de que horas são.
Decorrido certo intervalo de rempo, digamos, 5 s, você se encontra na posição 5 m, isto é, a cinco metros à direita do marco zero. Para um intervalo genérico de tempo, vamos chamar a sua nova posição de $S$ e o novo instante de $t$. Caso você ande sempre a mesma distância no mesmo intervalo de tempo (por exemplo, no caso acima você andou oito metros em cinco segundos, assim se adasse mais 8 m, demoraria os mesmo 5 s ou demoraria 2,5 s para andar 4 m e assim por diante), então dizemos que possui velocidade constante e portanto apresenta um Movimento Uniforme.
Dizemos então que o deslocamento do corpo em nosso referencial é igual à $S - S_0$ e à isso damos o nomes de $\Delta S$; o tempo decorrido foi de $t-t_0$ e à isso damos o nome de $\Delta t$.
Assim, podemos definir o que é velocidade de um móvel: $$v=\frac{\Delta S}{\Delta t}$$ Assim, em nosso exemplo: $$v=\frac{\Delta S}{\Delta t}=\frac{S-S_0}{t-t_0}=\frac{5-(-3)}{5}\frac{m}{s}=\frac{8}{5}\frac{m}{s}$$ Observe que $\Delta t=5\text{ s}$ independente dos valores de $t$ e $t_0$. Observe também que estamos dividindo duas grandezas com unidades, assim a resposta deve se manter com unidade: $$v=1,6\text{m/s}$$
Sempre que você for resolver qualquer problema de cinemática, lembre-se de que O Referencial é Indispensável. Também é importante saber que o corpo possui velocidade constante, pois se não for, a relação anterior não é válida.
Agora suponha que você adote para $t_0$ o valor nulo, isto é, ao olhar para seu relógio você ligue o cronômetro (isso é apenas uma escolha de um referencial, pois pode-se adotar qualquer valor para $t_0$), assim a equação da velocidade pode ser reescrita: $$v=\frac{\Delta S}{\Delta t}=\frac{S-S_0}{t-t_0}=\frac{S-S_0}{t}\Rightarrow$$ $$vt=S-S_0\Rightarrow$$
| $$S=vt+S_0$$ |
Esta equação é nada mais nada menos do que a equação da reta. Compare: $$S=vt+S_0$$ $$y=\rm{a}x+b$$ Observe o gráfico abaixo e compare os dois casos:
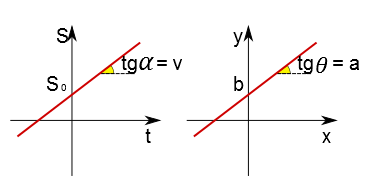
Na figura acima, são mostrados o coeficiente linear de ambos os gráficos ($b$ e $S_0$) e o coeficiente angular de ambos os gráficos ($\rm{a}$ e $v$). As propriedades que você conhecer da matemática poderão serem usadas aqui.
Assim, vimos que o gráfico que representa a posição de um corpo com Movimento Uniforme em função do tempo é uma reta. A equação da posição em função do tempo é chamada de Equação Horária da Posição. Assim se quisermos determinar em que posição um corpo estiver em qualquer (?) instante basta substituir o valor do temo na equação. Vamos então encontrar a equação horária para o exemplo acima.
Nós já encontramos a velocidade do corpo, que é $v=1,6\text{m/s}$; temos também a posição que ele se encontrava inicialmente: $S_0=-5\text{m}$; agora é só substituir na equação horária da posição: $$S=vt+S_0\Rightarrow$$ $$S=1,6t+(-3)\Rightarrow$$ $$S=1,6t-3$$
É de suma importância tomar cuidado com as unidades. Logo,como utilizamos o tempo em segundos e a posição em metros, a velocidade só poderá ser em $m/s$. O tempo que devemos utilizar na equação é em segundos assim como o resultado que iremos obter está em metros. O mesmo seria válido se usássemos o tempo em horas e a distância em quilômetros; ou o tempo em anos e a distância em milhas marítimas; e assim por diante.
Vamos lá, digamos que quero saber a posição do corpo no instante $t=12\text{s}$. Vamos substituir na equação: $$S=1,6t-3\Rightarrow$$ $$S=1,6\cdot12-3\Rightarrow$$ $$S=19,2-3\Rightarrow$$ $$S=16,2\text{m}$$ E esta é nossa resposta.
Mas e se $t<0$, o que podemos afirmar sobre este problema? Se compararmos com a equação de $y$ vs $x$ deveríamos acreditar que não há problema algum. Porém é necessário tomar cuidado, pois a observação começou no instante $t=t_0=0\text{s}$, logo nada podemos afirmar sobre qual era o comportamento do corpo antes deste instante. Na verdade, a equação horária obtida será válida, em geral, para tempos positivos, a menos que se possa garantir que o corpo já possuia este M.U. antes, mas ainda resta saber desde quando. Logo, as equações que obtivermos serão sempre limitadas e o nosso gráfico e equações horárias também.
Em geral, o gráfico correto para representar o M.U. será:
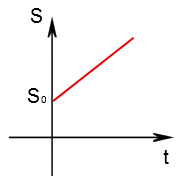
E a equação horária será: $$S=1,6t-3\text{ (S.I.) para t}\geq 0$$
O símbolo entre parênteses (S.I.) representa que as unidades de nossa equação está no Sistema Internadional, isto é, que a distância é medida em metros e que o tempo é medido em segundos.
Quando um corpo se move em um espaço tridimensional, e não em uma "reta real 'entortada' ", pensamos sempre em deslocamento vetorial. Assim, a velocidade e a posição serão dois vetores e a equação será semelhante à do caso escalar: $$\vec{v}=\frac{1}{\Delta t}\cdot\Delta \vec{S}=\frac{1}{t-t_0}\cdot (\vec{S}-\vec{S_0})$$
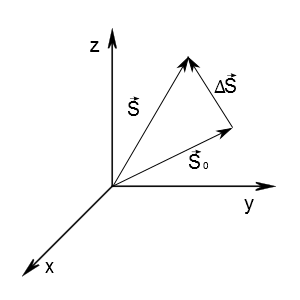
Verifique se faz sentido o esquema na figura acima. Perceba que: $$\vec{S_0}+\Delta \vec{S}=\vec{S}$$ ou equivalentemente, que: $$\Delta \vec{S}=\vec{S}-\vec{S_0}$$
Vamos para um Exemplo:
supondo que sejam dados: $$\left\{ \begin{matrix} \vec{S_0}=&\{2;1;0\} \text{m}\\ \vec{S}=&\{8;3;3\}\text{m} \\ \Delta t=&3,5\text{ s} \end{matrix}\right.$$ Calcule $\vec{v}$.
$$\vec{v}=\frac{\Delta \vec{S}}{\Delta t}\Rightarrow$$ $$\Delta \vec{S}=\vec{S}-\vec{S_0}=\{8;3;3\}-\{2;1;0\}\Rightarrow$$ $$\Delta \vec{S}=\{8-2;3-1;3-0\}=\{6;2;3\}$$ Logo: $$\vec{v}=\frac{1}{\Delta t}\cdot \{6;2;3\}\Rightarrow$$ $$\vec{v}=\frac{1}{3,5}\cdot \{6;2;3\}\Rightarrow$$ $$\vec{v}=\{\frac{6}{3,5};\frac{2}{3,5};\frac{3}{3,5}\}\text{ m/s}$$
Vamos agora encontrar a função horária na forma vetorial. Para isso, consideremos $t_0=0$ na equação da velocidade em sua forma vetorial: $$\vec{v}=\frac{\Delta \vec{S}}{\Delta t}\Rightarrow$$ $$\vec{v}=\frac{\vec{S} -\vec{S_0}}{t-t_0}\Rightarrow$$ $$\vec{v}=\frac{\vec{S} -\vec{S_0}}{t}\Rightarrow$$ $$t\cdot\vec{v}=\vec{S} -\vec{S_0}\Rightarrow$$
| $$\vec{S} =\vec{S_0}+\vec{v}\cdot t \; \; \; \text{ Equação Vetorial do M.U.}$$ |
Observe que se calcularmos o módulo dos dois lados desta equação, nós não obtemos a equação para o M.U. na sua forma escalar! Vejamos porque:
$$\vec{S} =\vec{S_0}+\vec{v}\cdot t\Rightarrow$$ $$|\vec{S} |=|\vec{S_0}+\vec{v}\cdot t|\Rightarrow$$ $$S=|\vec{S_0}+\vec{v}\cdot t|$$
Observe que o lado direito equivale à soma de dois vetores: o vetor posição inicial $S_0$ e o vetor velocidade multiplicado pelo escalar tempo, isto é, um outro vetor $\vec{v} t$ (que é equivalente à $t \vec{v}$). Como o módulo da soma de dois vetores não é igual à soma dos módulos dos vetores, não podemos obter um resultado igual ao da forma escalar. Ou seja: $$S_0+v\cdot t \neq|\vec{S_0}+\vec{v}\cdot t|$$
Continuando nosso exemplo, se quisermos calcular o módulo da velocidade, podemos fazer isso diretamente usando o vetor velocidade ou partirmos da nossa equação inicial da velocidade. Vamos fazer este último método e deixar o primeiro como exercício.
Observe que a equação a seguir possui equivalente ao da sua forma escalar: $$\vec{v}=\frac{1}{\Delta t}\cdot\Delta \vec{S}\Rightarrow$$ $$|\vec{v}|=\left |\frac{1}{\Delta t}\cdot\Delta \vec{S}\right |\Rightarrow$$ $$|\vec{v}|=\left |\frac{1}{\Delta t} \right | \cdot |\Delta \vec{S}|\Rightarrow$$ $$|\vec{v}|=\frac{1}{|\Delta t|} \cdot \Delta S \Rightarrow$$ $$v=\frac{\Delta S}{\Delta t} $$ Vamos então calcular $|\vec{\Delta S}|$: $$\Delta \vec{S}=\{6;2;3\}\Rightarrow$$ $$|\Delta \vec{S}|=\sqrt{6^2+2^2+3^2}\Rightarrow$$ $$|\Delta \vec{S}|=\sqrt{36+4+9}\Rightarrow$$ $$|\Delta \vec{S}|=\sqrt{49}\Rightarrow$$ $$|\Delta \vec{S}|= 7\text{ m}$$
Substituindo na equação da velocidade: $$v=\frac{\Delta S}{\Delta t} \Rightarrow$$ $$v=\frac{7}{\Delta 3,5} \Rightarrow$$ $$v=|\vec{v}|=2\text{ m/s}$$
Para finalisar, não confunda as duas grandezas distintas e que usamos os mesmos símbolos. São elas: $\Delta{S}=|\Delta \vec{S}|$ para o M.U. vetorial que é diferente de $\Delta S$ para o M.U. escalar; e $\Delta{v}=|\Delta \vec{v}|$ para o M.U. vetorial que é diferente de $\Delta v$ para o M.U. escalar.
Como já falamos de movimentos com velocidade constante, vamos agora considerar alguns trechos (sejam vetoriais ou escalares, mas por hora vamos pensar apenas na forma escalar) sendo que cada trecho é percorrido por um mesmo móvel com velocidades distintas, porém constantes. Vamos começar usando o exemplo a seguir:
Imagine que em um trecho retilíneo você faça marcações consecutivas entre dois pontos cuja localização do primeiro é $S_0$ e do segundo em $S$. Você divide este trecho em $n$ segmentos cada um com um comprimento que, medidos da esquerda para direita, possuem valores de $S_1$ para o primeiro, $S_2$ para o segundo e assim sucessivamente até o n-ésimo segmento de comprimento $S_n$. O primeiro segmento é percorrido por um móvel à uma velocidade $v_1$ e gasta-se um tempo $\\Delta t_1$; o segundo segmento é percorrido logo em seguida pelo mesmo corpo a uma velocidade $v_2$ gastando-se um tempo $\\Delta t_2$; o teceiro, $v_3$ em um tempo $\\Delta t_3$ e assim sucessivamente até o n-ésimo segmento que é percorrido a uma velocidade $v_n$ em um tempo $\\Delta t_n$. Aqui já se pode perceber que $\sum_{i=1}^{n} \Delta t_i=\Delta t$.
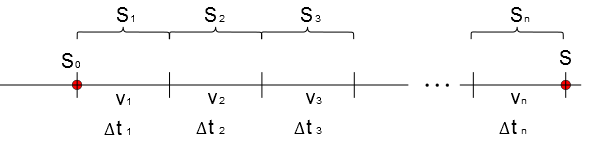
Vamos considerar três possibilidades:
Pergunta-se:
Em cada caso, qual deveria ser a velocidade de um segundo corpo para que ele percorra o trajeto inteiro a uma velocidade constante?
À esta velocidade constante damos o nome de Velocidade Média $V_M$.
Para o primeiro caso, temos: $$V_M=\frac{\Delta S}{\Delta t}\Rightarrow$$ $$V_M=\frac{\sum_{i=1}^{n} S_i}{\sum_{i=1}^{n} \Delta t_i}\Rightarrow$$ $$V_M=\frac{\sum_{i=1}^{n} v_i\cdot \Delta t_i}{n\cdot t}\Rightarrow$$ $$V_M=\frac{ t_i\sum_{i=1}^{n} v_i}{n\cdot t}\Rightarrow$$ $$\displaystyle V_M=\frac{\sum_{i=1}^{n} v_i}{n} \;\;\;\text{resultado para tempos iguais}$$
Este resultado é nada mais nada menos que uma média aritmética! Observe que, como $\Delta t$ é uma constante dentro do somatório, então $\sum_{i=1}^{n} \Delta t_i =\Delta t \cdot \sum_{i=1}^{n} 1$ e que o último termo é na veradade a soma do número 1 n vezes: $\sum_{i=1}^{n} 1 = n$
Agora, para o segundo caso obtemos: $$\displaystyle V_M=\frac{\Delta S}{\Delta t}\Rightarrow$$ $$\displaystyle V_M=\frac{\sum_{i=1}^{n} S_i}{\sum_{i=1}^{n} \Delta t_i}\Rightarrow$$ $$\displaystyle V_M=\frac{\sum_{i=1}^{n} S_i}{\displaystyle \sum_{i=1}^{n} \frac{S_i}{v_i}}\Rightarrow$$ $$\displaystyle V_M=\frac{n\cdot S}{\displaystyle \sum_{i=1}^{n} \frac{S}{v_i}}\Rightarrow$$ $$\displaystyle V_M=\frac{n\cdot S}{\displaystyle S\sum_{i=1}^{n} \frac{1}{v_i}}\Rightarrow$$
$$\displaystyle V_M=\frac{n}{\displaystyle \sum_{i=1}^{n} \frac{1}{v_i}}$$
Este resultado é uma Média Harmônica simples.
No último caso, vai depender dos dados que você possui. Por exemplo, se tiver a velocidade e o tempo para cada segmento, irá obter uma média aritmética ponderada pelos tempos (isto é, o tempo é o peso de cada velocidade):
|
$$V_M=\frac{\displaystyle \sum_{i=1}^{n} \Delta t_1 v_i}{\sum_{i=1}^{n} \Delta t_i}$$ |
Se tiver a velocidade e o comprimento de/em cada segmento, será uma média harmônica ponderada pela velocidade:
|
$$V_M=\frac{\displaystyle \sum_{i=1}^{n} S_i}{\sum_{i=1}^{n} \displaystyle\frac{S_i}{v_i}}$$ |
Se, por fim, souber o tempo e o comprimento de cada segmento, fica a fórmula mais simples e a que vocês mais utilizarão:
|
$$V_M=\frac{\displaystyle \sum_{i=1}^{n} S_i}{\sum_{i=1}^{n} \Delta t_i}$$ |
Ela pode ser reescrita como: $$V_M=\frac{\Delta S}{\Delta t}$$
Em sua forma vetorial, a velocidade média não será diferente:
$$\vec{V_M}=\frac{\Delta \vec{S}}{\Delta t}$$
Vamos agora ver como calcular velocidade relativa. Apresentaremos este assunto em uma abordagem vetorial e a sua consequência escalar, que é o método geralmente empregado, será imediata.
Suponha que existam dois móveis, A e B, com velocidades $\vec{v_A}$ e $\vec{v_B}$ conhecidas, conforme esquema abaixo:
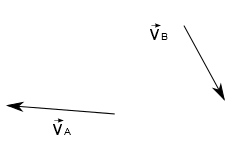
Você quer saber qual a velocidade de B em relação à A. Para isso, você sabe de antemão que A está parado em relação à ele mesmo, logo para que o vetor velocidade se anule, podemos simplesmente somar à velocidade de A o vetor $-\vec{v_A}$. Para mantermos coerência, isto é, para que B adquira uma velocidade compatível ao novo referencial, precisamos somar o vetor $-\vec{v_A}$ ao vetor $\vec{v_B}$:
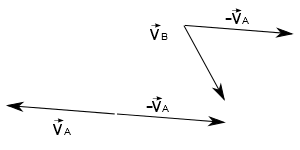
Assim, basta obter o novo vetor:
| $$\vec{v_{BA}}=\vec{v_B}-\vec{v_A}$$ |
Caso você tenha n corpos, cada um com uma velocidade diferente, basta somar $-\vec{v_A}$ à TODOS os vetores velocidades de TODOS os corpos, os quais você deseja saber a velocidade no referencial de A.
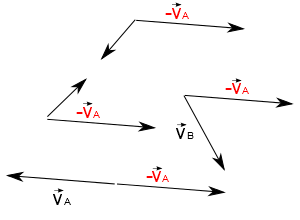
Alternativamente, a velocidade do móvel pode ser obtida geometricamente pela soma vetorial:
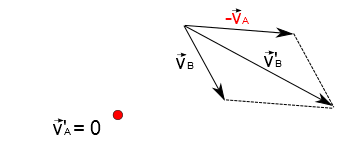
Aqui $$\vec{v_{AB}}=\vec{v'_B}$$
Agora pode-se verificar a relação de velocidade relativa em uma dimensão. Por exemplo, se os dois corpos tiverem indo na mesma direção, pode-se ver que o módulo da velocidade relativa é a diferênça dos módulos dos dois vetores. Lembre-se do caso de diferênça de vetores quando o ângulo entre eles for de 180$^o$. Por exemplo: se um veículo anda a 15 km/h e o outro à 20 km/h, então o módulo da diferênça dos vetores velocidade será de 15 km/h e esta será a velocidade relativa entre ambos os móveis. Perceba também que o módulo da velocidade de um móvel A em relação à um outro móvel B é igual ao módulo da velocidade do móvel B em relação ao móvel A.
Caso os dois móveis estejam se dirigindo um contra o outro, então a diferênça entre os dois vetores velocidade é a soma dos seus módulos.
Para treinar, tente representar o que está descrito nos dois parágrafos anteriores. Convença-se de que isso faz sentido e de que a "regra" da soma de velocidades quando os móveis se aproxima um contra o outro e a "regra" da diferênça que se é usada quando os móveis estão se dirigindo no mesmo sentido são na verdade um caso particular da equação da velocidade relativa na sua forma vetorial!
Resumindo: $$\vec{v_{BA}}=\vec{v_B}-\vec{v_A}$$ $$\vec{v_{AB}}=\vec{v_A}-\vec{v_B}$$
Vamos agora estudar dois casos especiais. O primeiro diz respeito ao alinhamento de corpos em movimento e o segundo está relacionado ao cálculo de velocidade mínima para, digamos, atravessar um rio com correnteza em dada direção.
Vamos começar aqui com o alinhamento de corpos. Comecemos com um exemplo: o problema das velas que aparece em muitos livros, como o Saraeva e Renato Brito, que foram sugeridos no primeiro link.
Vejamos o problema:
Em um momento inicial duas velas eram iguais e tinham altura $h$, encontrando-se a uma distância $\rm{a}$. A distância entre cada uma das velas e a parede mais próxima é também igual a $\rm{a}$.
Com que velocidade movem-se as sombras das velas nas paredes, se uma vela queima durante o tempo $t_1$ e a outra durante o tempo $t_2$?
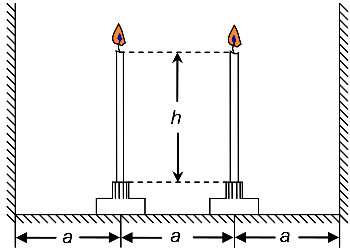
Podemos resolver este problema de duas formas: uma geométrica (por semelhança de triângulos) e outra usando determinantes (analiticamente). Vamos resolver pelos dois métodos:
SOLUÇÃO 1: SEMELHÂNÇA DE TRIÂNGULOS
Imagine um instante $t$, com $t_0=0$, depois de iniciada a queima da vela. Vamos considerar as chamas como sendo pontuais e situadas imediatamente acima de cada uma das velas.
A figura a seguir representa esta situação.
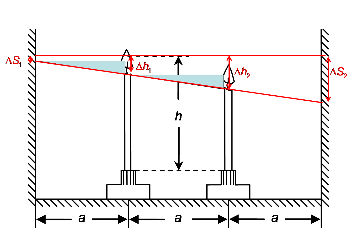
Na figura também estão representados dois triângulos pequenos que são semelhantes. Vamos então utilizar este fato para encontrar a velocidade da sombra da esquerda, que chamaremos de $v_1$.
Observe que a base de ambos os triângulos são iguais à $\rm{a}$, mas as alturas são diferentes. Para o triângulo da esquerda, a altura é $$\Delta h_1-\Delta S_1 $$ enquanto que a altura do triângulo da direita será: $$\Delta h_2-\Delta h_1 $$
Fazendo então a semelhânça, temos: $$\frac{\Delta h_2-\Delta h_1 }{rm{a}}= \frac{\Delta h_1-\Delta S_1 }{\rm{a}}\Rightarrow$$ $$\Delta h_2-\Delta h_1= \Delta h_1-\Delta S_1$$ Entretanto podemos escrever os deslocamentos das velas como função do tempo, pois sabemos a velocidade de cada vela: $$v_{vela1}=\frac{h}{t_1}$$ $$v_{vela2}=\frac{h}{t_2}$$ Dividindo-se a equação inteira pelo tempo $t$ obtemos: $$v_{vela2}-v_{vela1}= v_{vela1}-v_{sombra1}\Rightarrow$$ $$v_{sombra1}= 2v_{vela1}-v_{vela2}$$
Substituindo as velocidades: $$v_{sombra1}= 2\frac{h}{t_1}-\frac{h}{t_2}\Rightarrow$$
| $$v_{sombra1}= h\left(\frac{2t_2-t_1}{t_1\cdot t_2} \right )$$ |
Observe que se $t_1>2t_2$ então obtemos um sinal negativo para a velocidade da sombra, o que significa que a sobra possui sentido oposto ao que nós suposmo. Agora de $2t_2>t_1$ então a velocidade da sombra está para baixo, que é o sentido que escolhemos.
Vamos agora determinar a velocidade da outra sobra na outra parede. Para isso temos que encontrar quaisquer outros dois triângulos semelhantes que possuam apenas uma informação desconhecida, no caso, seria $\Delta S_2$. Veja os triângulos abaixo que eu escolhi (outros também podem dar certo):
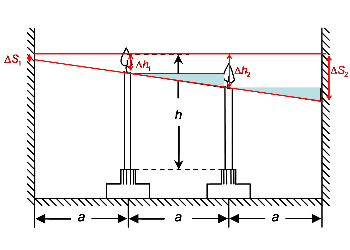
Fazendo uma semelhança parecida com o caso anterior, obtemos: $$\frac{\Delta h_2-\Delta h_1 }{\rm{a}}= \frac{\Delta S_2-\Delta h_2 }{\rm{a}}\Rightarrow $$ $$\Delta h_2-\Delta h_1 =\Delta S_2-\Delta h_2 \Rightarrow$$ Dividindo por $t$: $$v_{vela2}-v_{vela1} =v_{sombra2}-v_{vela2} \Rightarrow$$ $$\frac{h}{t_2}-\frac{h}{t_1} =v_{sombra2}-\frac{h}{t_2} \Rightarrow$$
$$v_{sombra2}=2\frac{h}{t_2}-\frac{h}{t_1} \Rightarrow$$| $$v_{sombra2}=h\left ( \frac{2t_1-t_2}{t_1\cdot t_2} \right )$$ |
Até aqui o que você deve ter apreendido com este exemplo, é que você deve sempre encontrar pelo menos dois triângulos semelhantes, e a partir daí, tentar relacionar com os demais dados do enunciado
Abaixo, apresentaremos um método analitico que, de certo modo, você terá "que pensar menos", pois basta jogar em uma matriz, encontrar o determinante e igualar à zero. O melhor método para você será o que você se adapatar melhor.
SOLUÇÃO 2: MATRIZ E DETERMINANTE
Você deve se lembrar da condição de alinhamento de três pontos que provavelmente já viu na matemática: dados três pontos não coincidentes A$(x_A;y_A)$, B$(x_B;y_B)$ e C$(x_C;y_C)$, eles serão alinhados se, e somente se, o determinante da matriz abaixo for nulo: $$\begin{bmatrix} x_A & y_A & 1\\ x_B & y_B & 1\\ x_C & y_C & 1 \end{bmatrix}$$ Ou seja: $$\text{det}\begin{bmatrix} x_A & y_A & 1\\ x_B & y_B & 1\\ x_C & y_C & 1 \end{bmatrix} =0 $$
A figura a seguir representa a situação do nosso problema. Nela também foi adicionado um par de eixos formando um sistema cartesiano, para que assim possamos usar a propriedade acima.
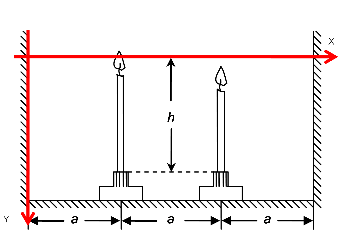
Basta então resolvermos o determinante colocando as coordenadas de cada um de nossos pontos de interesse. Observe que os nosso pontos A, B e C são respectivamente a localização da inteface de uma das sombras (por exemplo a da esquerda de coordenadas $(0;v_{sombra1}\cdot t)$), da vela da esquerda $(\rm{a};v_{vela1}\cdot t)$ e da vela da direita $(\rm{2a};v_{vela2}\cdot t)$. Observe também que temos que valcular o determinate usando sempre três pontos, sendo dois conhecidos e apenas um desconhecido. Temos então que resolver dois determinantes, mas farei apenas o cálculo da sombra da esquerda e deixarei o da direita como exercício: $$ \text{det}\begin{bmatrix} 0 & v_{sombra1}\cdot t & 1\\ \rm{a} & v_{vela1}\cdot t & 1\\ \rm{2a} & v_{vela2}\cdot t & 1 \end{bmatrix} = \text{det}\begin{bmatrix} 0 & v_{sombra1}\cdot t & 1\\ \rm{a} & \displaystyle \frac{h}{t_1}\cdot t & 1\\ \rm{2a} & \displaystyle \frac{h}{t_2}\cdot t & 1 \end{bmatrix} =0 $$
Calculando o determinate (se não se lembra de como fazer, recomendo que procure na internet ou em algum livro de sua preferência, pois lhe será muito útil): $$ \text{det}\begin{bmatrix} 0 & v_{sombra1}\cdot t & 1\\ \rm{a} & \displaystyle \frac{h}{t_1}\cdot t & 1\\ 2\rm{a} & \displaystyle \frac{h}{t_2}\cdot t & 1 \end{bmatrix} =0+v_{sombra1}\cdot t\cdot 2\rm{a}+\displaystyle \frac{h}{t_2}\cdot t\cdot \rm{a}-\displaystyle \frac{h}{t_1}\cdot t\cdot 2\rm{a}-0-v_{sombra1}\cdot t\cdot \rm{a} =0 $$ $$v_{sombra1}\cdot 2+\displaystyle \frac{h}{t_2}\cdot -\displaystyle \frac{h}{t_1}\cdot 2-v_{sombra1}=0$$ $$ $$
| $$v_{sombra1}= h\left(\frac{2t_2-t_1}{t_1\cdot t_2} \right )$$ |
Confira passo a passo as operações acima. Caso não tenha entendido, procure voltar e reler quantas vezes forem necessárias.
Faça os cálculos para a sombra da esquerda e confira se a resposta é igual à obtida pelo método geométrico.
Digamos agora que você tem o seguinte problema:
Um ônibus move-se numa estrada com velocidade $V_1 = 16$m/s. Um homem encontra-se a uma distância $x = 60$m da estrada e $y = 400$m do ônibus. Qual o módulo da mínima velocidade $V_2$ que o homem deve correr para alcançar o ônibus?
Perceba primeiramente que o problema se resume ao que está esquematizado a seguir:
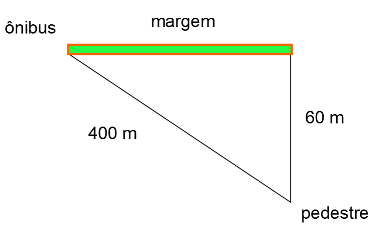
Observe também que a distância de 400 m mencionada no texto é a distância entre o observador e o ônibus, e não ao longo da margem da rodovia.
Para resolver este problema você pode "apelar" para a velocidade relativa, obviamente em sua forma vetorial! Pois esta é a forma que acabamos de ver. Assim, vamos mudar para o referêncial de algum passageiro parado em relação ao ônibus, ou seja, vamos somar $-\vec{v}_{ônibus}=-\vec{V}_1$ ao vetor velocidade do ônibus e também do homem.
A figura abaixo apresenta o vetor velocidade do ônibus somado ao vetor velocidade do homem, que ainda não sabemos nada a respeito da direção nem da velocidade.
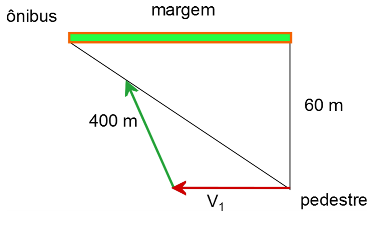
Entretanto, há uma informação muito importante na figura que já sabemos de antemão: no novo referencial, isto é, relativamente ao ônibus, o homem deve caminhar em uma linha reta diretamente em sua direção, assim sabemos que a soma do vetor $-\vec{V}_1$ ao vetor velocidade do homem $\vec{V}_2$ devemos obter um vetor cuja direção é ao longo da reta que liga o homem ao ônibus. Por isso sabemos que a figura assima pode não minimizar a velocidade, mas certamente ele alcançará o ônibus.
Mas o pobre homem tem problemas cardíacos, e deve correr o mínimo possível, então o vetor velocidade $\vec{v}_2$ deve ser o mínimo, fazendo com que a resultante seja ao longo da reta homem-ônibus. Assim, veja que para que o vetor seja mínimo, ele deve formar um ângulo de 90$^o$ com tal direção, conforme o esquema abaixo:
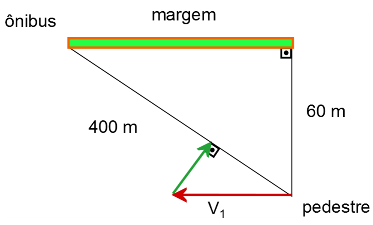
Observe a figura abaixo na qual os vértices dos triângulos foram nomeados e foi adicionado dois ângulos congruentes (alternos internos).
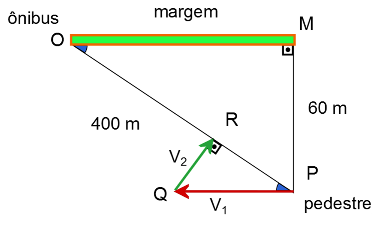
Usando os dois vetores velocidade que compõem o triângulo PQR, podemos usando semelhança de triângulos pelo critério ângulo-lado-lado, calcular $\vec{v}_2$:
$$\frac{v_1}{v_2}=\frac{400}{60}\Rightarrow$$ $$v_2=\frac{3}{20}\cdot v_2 \Rightarrow $$ $$v_2=\frac{3}{20}\cdot 16 \Rightarrow $$
| $$v_2=2,4\text{ m/s}$$ |
Mas este não deve ser um exercício vazio: o que você deve ter em mente é que através de argumentos puramente geométricos (vetores) pode-se encontrar uma velocidade mínima para o homem encontrar com o ônibus.
Exitem outras aplicações como travessia de rios. Você consegue imaginar algum exemplo?
Bons Estudos à todos!